格密码
线性代数前置知识
先回顾一下学校线代课程讲过的几个概念
向量空间
设\(V\)是 n 元向量的集合,如果\(V\)非空,并且对于向量的线性运算封闭(即对任意 \(\boldsymbol{v_1} \in V,\boldsymbol{v_2} \in V,k \in \mathbb{R}\) ,都有 \(\boldsymbol{v_1+v_2} \in V,k\boldsymbol{v_1} \in V\) ),则称 \(V\) 是一个向量空间。
向量空间的基与维数
向量空间\(V\)的一个极大无关组叫做\(V\)的一个基,\(V\) 的秩叫做\(V\)的维数,记作\(dim(V)\)。若 \(dim(V)=r\),则称\(V\)为\(r\)维向量空间。
若已知\(r\)维向量空间\(V\)的基为\(\boldsymbol{v_1,v_2,\cdots,v_r}\),则向量空间\(V\)可以表示成
\[ V=\{ \boldsymbol{v}=x_1\boldsymbol{v_1}+x_2\boldsymbol{v_2}+\cdots +x_r\boldsymbol{v_r} | x_1,x_2,\cdots,x_r \in \mathbb{R}\} \]
向量正交与施密特(Schmidt)正交化
当\(\boldsymbol{a\neq 0,b\neq 0}\)时,当\((\boldsymbol{a,b}=0)\),即\(\boldsymbol{a^Tb}=0\)时,称向量\(\boldsymbol{a,b}\)正交。
由两两正交的非零向量组成的向量组称为正交向量组,由单位向量组成的正交向量组称为标准正交向量组。
\(n\)维欧氏空间求解正交基,一组基底为\((\alpha_1,\alpha_2,\cdots,\alpha_n)\)
- Step1:令 \(\beta_1=\alpha_1\)
- Step2:计算\(\alpha_2\)在\(\beta_1\)方向上的投影,并做差得到 \[\beta_2=\alpha-\frac{(\beta_1,\alpha_2)}{(\beta_1,\beta_1)}\beta_1\]
- Step3:计算\(\alpha_3\)在向量\(\beta_1,\beta_2\)方向的投影,继续做差得到\(\beta_3\)
格
\(n\)元向量的集合 \(v_1,\cdots,v_n \in \mathbb{R}^n\),格(Lattices)就是这些向量的线性组合
\[L=\{a_1v_1+a_2v_2+\cdots+a_nv_n \mid a_1,a_2,\cdots,a_n \in \mathbb{Z}\}\]
对比向量空间的定义,可以发现系数是整数,因此定义出来的格空间是一些格点,而非连续的向量空间。
下图是一个二维格,平行四边形的一组邻边是格的基底。通过对这两个向量不断进行线性组合,那么就产生了很多格点,就形成了一个格。
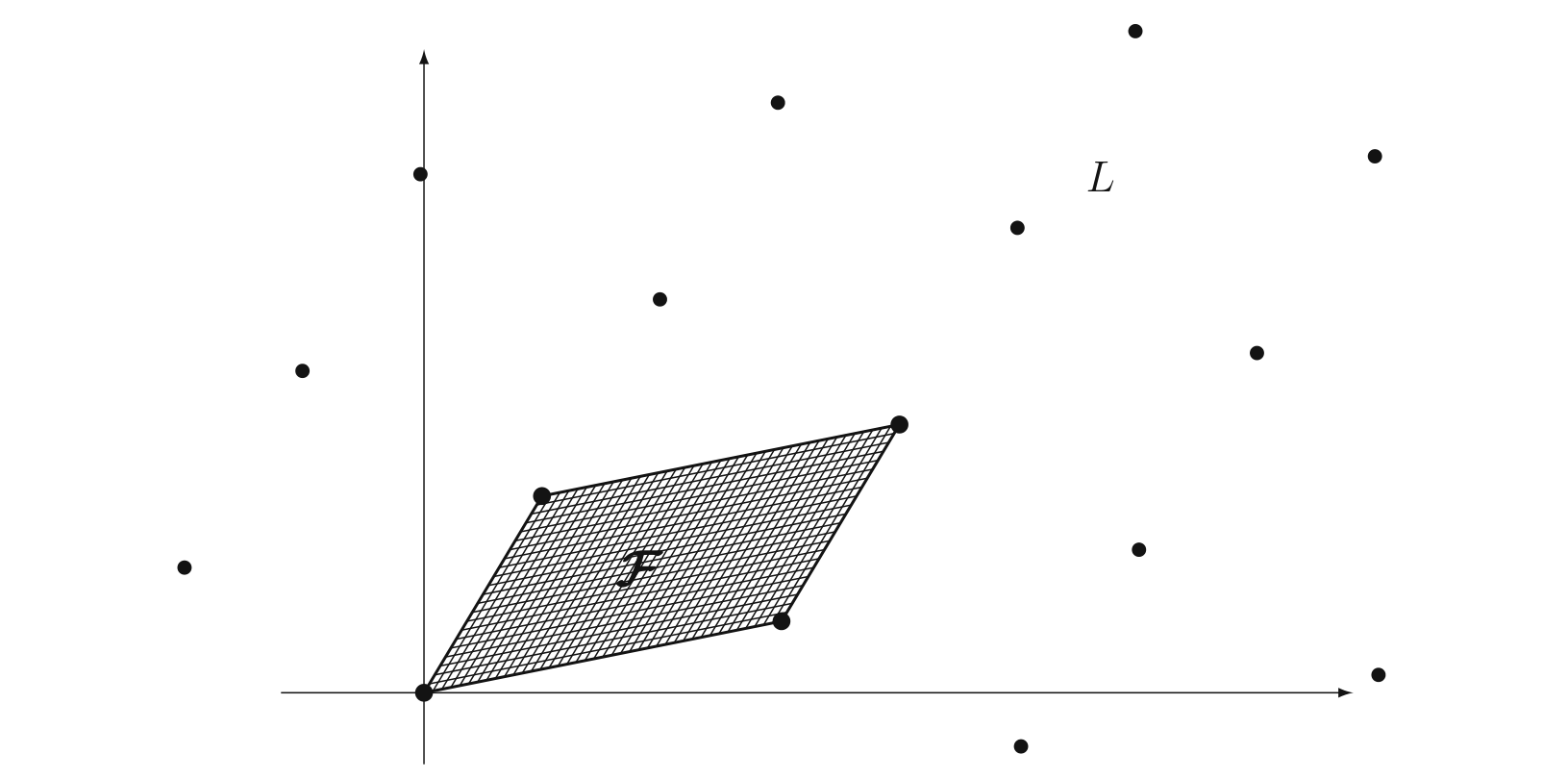
基本域
假定 \(v_1,v_2,\cdots,v_n\) 是格 \(L\) 的基,\(F\{v_1,v_2,\cdots,v_n\}=\{a_1v_1+a_2v_2+\cdots+a_nv_n \mid a_1,a_2,\cdots,a_n \in [0,1]\}\)
上图中的平行四边形,就是二维格中一组基底构成的基本域。
格基本域的体积等于格的行列式的值,基本域的体积就是积分,而这也正是行列式的几何意义,\(Volume(F\{v_1,v_2,\cdots,v_n\})=det(L)\)
矩阵表示
假定 \(v_1,v_2,\cdots,v_n\) 是格 \(L\) 的基,\(w_1,w_2,\cdots,w_n \in L\),则必然存在整系数 \(a_{ij}\) 使得:
\[ \begin{cases} w_1=a_{11}v_1+a_{12}v_2+\cdots+a_{1n}v_n \\ w_2=a_{21}v_1+a_{22}v_2+\cdots+a_{2n}v_n \\ \vdots \\ w_n=a_{n1}v_1+a_{n2}v_2+\cdots+a_{nn}v_n \end{cases} \]
可以提取出一个系数矩阵
\[ A= \begin{bmatrix} a_{1,1} & a_{1,2} & \ldots & a_{1,n}\\ a_{2,1} & a_{2,2} & \ldots & a_{2,n}\\ \vdots & \vdots & \ddots & \vdots \\ a_{n,1} & a_{n,2} & \ldots & a_{n,n} \end{bmatrix} \]
进而将上述方程组转换为矩阵表示\(\boldsymbol{w}=A * \boldsymbol{v}\)
LLL/BKZ 算法
之前打国际赛看到 discord 里一直有人赞美 flatter,应该是加速 LLL 用的,我还没配好环境。
一种格基约简算法,可以找到格上的一组最短的正交基。
在Sagemath中可以直接调用函数。
但对于函数的实现以及算法的原理没必要深究,在具体题目当中会使用即可。
1 | |
下图是高斯启发式,为我们展示了格上最短向量的欧几里得范数的大致范围。

这样我们就知道构造出来的格,是否可以规约出我们的目标向量,也为我们调整格的平衡提供了思路。接下来我们在以下几个问题当中具体看一下LLL算法的应用。
lattice 应用
下面将首先介绍两个最基本问题SVP和CVP,这是格上的两个困难问题,都属于
NP 完全问题。因此在这两个困难问题上也将延伸出很多格密码体系。
SVP
最短向量问题(Shortest Vector Problem,SVP)
这是最基本的一个问题,后续很多格问题最终都转换成了SVP问题,从LLL算法中我们也可以看出,最终得到的是格上的最短正交向量组。
下面从一个例子来介绍格的构造和 LLL 的应用。
1 | |
\[(p*f - 58 * f + q) \% g = 44\] \[k\cdot g+44=(p-58)\cdot f+q\] 我们目的是通过\(f,g\)求出\(p,q\),从代码的定义可以看到,\(p,q\)的位数相比于\(f,g\)来说很小,因此可以应用格的思路,构造一个合适的格,规约出\((p,q)\)
写出如下方程组 \[k\cdot g-(p-58)\cdot f=q-44\] \[k\cdot 0-(p-58)\cdot (-1)=p-58\] 可以看到第二个式子是一个恒等式,在构造格时我们通常需要加入这样的恒等式。
下面将方程组转换为矩阵。
\[(k, p-58) \begin{bmatrix}0&g\\1&-f \end{bmatrix}=(p-58,q-44)\]
得到了\(v*B=w\)的形式。在这个式子中我们关心的是\(w\)向量是否是格\(B\)上的最短向量,\(v\)这是线性组合的系数并不用过多关注。
在介绍高斯启发式的时候,提到了格上最短向量的欧几里得范数的大致范围,我们现在验证一下,看看\(w\)是否是格\(B\)上的最短向量,即比较长度\(||w||\)和高斯期望值\(\sigma(det(B))\)
\[||w|| = \sqrt{(p-58)^2+(q-44)^2}\approx 2^{1024}\] \[\sigma(det(B))\approx det(B)^{1/2}=\sqrt{g}\approx 2^{1024}\]
于是\(w\)大概率为格\(B\)上的最短向量,构造格\(B\)进行LLL算法即可。
还有个例子可以看背包加密
CVP
最近向量问题(Closest Vector Problem),格上另一个最常见的问题。
给定格\(L\)的一组基与向量\(v\),找到在\(L\)上离\(v\)最近的一个向量。
方便理解还是看一下几何意义,在连续空间中任找一点\(p\)(注意:不一定在格上),要找到格上距离点\(p\)最近的一个点。
LWE
LWE 问题(Learn With Error)
ACD
ACD 问题(Approximate Common Divisor),近似公约数(应该也可以叫 AGCD)
给定\(t\)组\(x_i\)满足:\(x_i=pq_i+r_i\)
\(x_i\) 已知,\(p\) 为 \(\alpha\) 位,\(q_i\) 为 \(\beta\) 位 ,\(r_i\) 为 \(\rho\) 位(\(\rho \lt\lt \alpha\)),求 \(p\)。
\(p\)相当于\(t\)组\(x\)的近似公约数,因此要求了\(r_i \lt\lt p\)
构造
\[(q_0,q_1,\cdots,q_t)\begin{bmatrix} 2^{\rho} & x_1 & x_2 & \cdots & x_t \newline 0 & -x_0 & 0 & \cdots & 0 \newline 0 & 0 & -x_0 & \cdots & 0 \newline \vdots & \vdots & \vdots & \ddots & \vdots \newline 0 & 0 & 0 & \cdots & -x_0\end{bmatrix}=(q_02^{\rho},q_0x_1-q_1x_0,\cdots,q_0x_t-q_tx_0)=(q_02^{\rho},q_0r_1-q_1r_0,\cdots,q_0r_t-q_tr_0)\]
记为 \(v\cdot B=w\)。
使用LLL算法得到 \(q_02^{\rho}\)后就可以求出\(p\)。