2022祥云杯wp-crypto

little little fermat

题目源码

from Crypto.Util.number import *
from random import *
from libnum import *
import gmpy2
from secret import x

flag = b'?????????'
m = bytes_to_long(flag)
def obfuscate(p, k):
    nbit = p.bit_length()
    while True:
        l1 = [getRandomRange(-1, 1) for _ in '_' * k]
        l2 = [getRandomRange(100, nbit) for _ in '_' * k]
        l3 = [getRandomRange(10, nbit//4) for _ in '_' * k]
        l4 = [getRandomRange(2, 6) for _ in '_' *k]
        A = sum([l1[_] * 2 ** ((l2[_]+l3[_])//l4[_]) for _ in range(0, k)])
        q = p + A
        if isPrime(q) * A != 0:
            return q

p = getPrime(512)
q = obfuscate(p, 5)
e = 65537
n = p*q
print(f'n = {n}')

assert 114514 ** x % p == 1
m = m ^ (x**2)
c = pow(m, e, n)
print(f'c = {c}')

'''
n = 141321067325716426375483506915224930097246865960474155069040176356860707435540270911081589751471783519639996589589495877214497196498978453005154272785048418715013714419926299248566038773669282170912502161620702945933984680880287757862837880474184004082619880793733517191297469980246315623924571332042031367393
c = 81368762831358980348757303940178994718818656679774450300533215016117959412236853310026456227434535301960147956843664862777300751319650636299943068620007067063945453310992828498083556205352025638600643137849563080996797888503027153527315524658003251767187427382796451974118362546507788854349086917112114926883
'''

题目分析

根据题目名字来看，此题和费马小定理的使用有关，题目中有一个obfuscate函数，进行了对q的生成，q=p+A，这里可以看一下A的范围，是在2^[18,319]之间，因此p、q接近，尝试一下yafu分解。

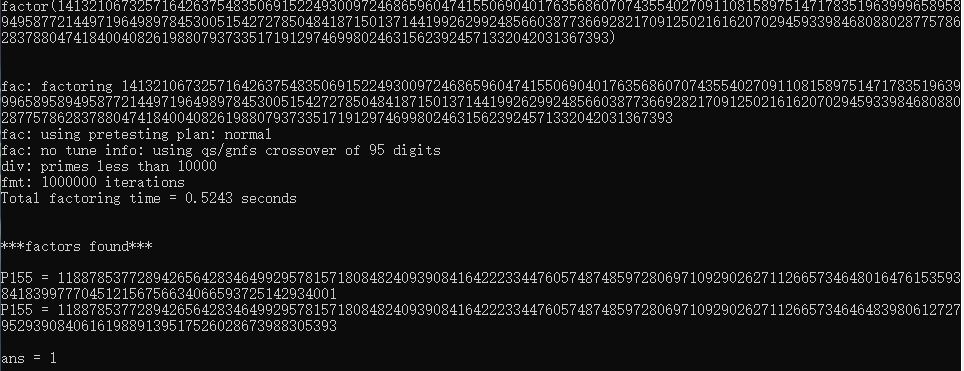题目对m先进行了处理，再进行RSA加密，因此我们需要知道x。assert 114514 ** x % p == 1运用费马小定理，若114514与p互素，则x=p-1，即可求解m。

EXP

from Crypto.Util.number import *
import gmpy2
import math
e=65537
n = 141321067325716426375483506915224930097246865960474155069040176356860707435540270911081589751471783519639996589589495877214497196498978453005154272785048418715013714419926299248566038773669282170912502161620702945933984680880287757862837880474184004082619880793733517191297469980246315623924571332042031367393
c = 81368762831358980348757303940178994718818656679774450300533215016117959412236853310026456227434535301960147956843664862777300751319650636299943068620007067063945453310992828498083556205352025638600643137849563080996797888503027153527315524658003251767187427382796451974118362546507788854349086917112114926883
p = 11887853772894265642834649929578157180848240939084164222334476057487485972806971092902627112665734648016476153593841839977704512156756634066593725142934001
q = 11887853772894265642834649929578157180848240939084164222334476057487485972806971092902627112665734646483980612727952939084061619889139517526028673988305393
print(math.gcd(p,114514))
#1
x=p-1
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m0=pow(c,d,n)
m=m0^(x**2)
print(long_to_bytes(m))
#flag{I~ju5t_w@nt_30_te11_y0u_how_I_@m_f3ll1ng~}

fill

题目源码

from Crypto.Util.number import *
from random import *
from gmpy2 import gcd
from numpy import dot

nbits = 32
msg = getRandomNBitInteger(nbits)
flag = b'flag{sha256(msg)}'
tmp_m = bin(msg)[2:]
f_list = []
for i in range(len(tmp_m)):
    f_list.append(int(tmp_m[i]))

r_list =[randint(20, 50)]
for i in range(nbits - 1):
    r_list.append(randint(2 * r_list[-1], 3 * r_list[-1]))

while True:
    A = randint(2 * r_list[-1] + 1, 3 * r_list[-1])
    B = randint(2 * r_list[-1] + 1, 3 * r_list[-1])
    if gcd(A, B) == 1:
        break

M = [A * x % B for x in r_list]

S = dot(f_list, M)
print(S)

seed = getRandomNBitInteger(30)
s = [0] * nbits
s[0] = seed
m = getRandomNBitInteger(20)
c = getPrime(24)
n = 991125622
for i in range(1, nbits):
    s[i] = (s[i-1]*m+c)%n
print(s[0], s[1], s[2])
for t in range(nbits):
    M[t] = M[t] + s[t]
print(M)


'''
492226042629702
562734112 859151551 741682801
M = [19621141192340, 39617541681643, 3004946591889, 6231471734951, 3703341368174, 48859912097514, 4386411556216, 11028070476391, 18637548953150, 29985057892414, 20689980879644, 20060557946852, 46908191806199, 8849137870273, 28637782510640, 35930273563752, 20695924342882, 36660291028583, 10923264012354, 29810154308143, 4444597606142, 31802472725414, 23368528779283, 15179021971456, 34642073901253, 44824809996134, 31243873675161, 27159321498211, 2220647072602, 20255746235462, 24667528459211, 46916059974372]
'''

题目分析

随机产生32位的数，sha256()加密后作为flag，并将其2进制的每一位存到了f_list数组中。

又 创建了一个r_list32位数组，里面存着随机数，先暂时不管。

双 对r_list数组中的随机数做了加密，产生了M数组。

对f_list和M数组进行了numpy.dot运算，即向量乘法，得到和为S。

叒 创建了一个s数组，这个很明显，用LCG线性同余算法进行了加密。

最后将M数组与s数组相加。

这就是这道题整体的流程，每一步并不难，只是步骤多，略显复杂。

EXP

0x01

可以先进行一下LCG的求解，把s数组求解出来，从而求出M数组。

n = 991125622
output =[562734112,859151551,741682801]
MMI = lambda A, n,s=1,t=0,N=0: (n < 2 and t%N or MMI(n, A%n, t, s-A//n*t, N or n),-1)[n<1] #逆元计算
a=(output[2]-output[1])*MMI((output[1]-output[0]),n)%n
ani=MMI(a,n)
b=(output[1]-a*output[0])%n

seed = 562734112
a=55365664
b= 8712091
s = [0] * nbits
s[0] = seed
for i in range(1, nbits):
    s[i] = (s[i-1]*a+b)%n
M = [19621141192340, 39617541681643, 3004946591889, 6231471734951, 3703341368174, 48859912097514, 4386411556216, 11028070476391, 18637548953150, 29985057892414, 20689980879644, 20060557946852, 46908191806199, 8849137870273, 28637782510640, 35930273563752, 20695924342882, 36660291028583, 10923264012354, 29810154308143, 4444597606142, 31802472725414, 23368528779283, 15179021971456, 34642073901253, 44824809996134, 31243873675161, 27159321498211, 2220647072602, 20255746235462, 24667528459211, 46916059974372]
for t in range(nbits):
    M[t] = M[t] - s[t]

0x02

按理来说，感觉应该根据求出来的M数组进行逆运算，求出r_list数组，但是求出来r_list有什么用呢，所以直接尝试求f_list。因为f_list中不是0就是1，与M做向量乘法，即为M数组中若干元素的和。根据题目给定和S，先大概看一下需要M中多少个元素累加。发现在M前21位和 < S，前22位和 > S，所以猜想应该是M当中，除10个左右元素之外的和。

这里就遍历了一下，复杂度实在太高了，也没想着能出，结果还真算出来了o.O

 for a in range(nbits):
     for b in range(a,nbits):
         for c in range(b,nbits):
             for d in range(c,nbits):
                 for e in range(d,nbits):
                     for f in range(e,nbits):
                         for g in range(f,nbits):
                             for h in range(g,nbits):
                                 for i in range(h,nbits):
                                     for j in range(i,nbits):
                                         for k in range(j,nbits):
                                             if M[a]+M[b]+M[c]+M[d]+M[e]+M[f]+M[g] +M[h] + M[i] +M[j] +M[k] == sum-S:
                                                 print(a,b,c,d,e,f,g,h,i,j,k)
                                                 break
#2 4 9 10 15 19 24 27 28 30 31

也就说明，f_list中下标为这些的，对应值是0，其余为1，即可得到msg的2进制数，转为十进制后进行sha256()加密即可。

f = ['1'] * nbits
f[2]=f[4]=f[9]=f[10]=f[15]=f[19]=f[24]=f[27]=f[28]=f[30]=f[31]='0'
a=""
for i in range(nbits):
    a+=f[i]
print(int(a,2))
#3617517412
#sha256加密后：8f504aee71626212f275117326722b6c0ccc94f4039ed31fbcfde08e026352c4，套上flag{}提交即可